Bayes Rules! Chapter 9 Exercises

Quest into the Bayesian realm.
Author

Farhan Reynaldo Hutabarat

Published

September 25, 2022

Conceptual exercises

Exercise 9.1 (Normal regression priors)

For the Normal regression model (9.6) with \(Y_i | \beta_0, \beta_1, \sigma \sim N(\mu_i, \sigma)\) where \(\mu_i = \beta_0 + \beta_1 X_i\), we utilized Normal priors for \(\beta_0\), \(\beta_1\) and an Exponential prior on \(\sigma\).

  1. Why is a Normal prior a reasonable choice for \(\beta_0\) and \(\beta_1\)?
  2. Why isn’t a Normal prior a reasonable choice for \(\sigma\)?
  3. What’s the difference between weakly informative and vague priors?

Answer

  1. Since the slope of the line could be any positive or negative value. In other words, it could positively or negatively affected the outcome variable.
  2. The standard deviation in the model must be positive, so it’s not reasonable to choose Normal prior, which could take negative value.
  3. While the vague prior might include a non-sensible values, the weakly informative has more sensible values. For instance, choosing a vague prior might include a possibility that an increase of 1 degree celsius could increase the sales of an ice cream by 100,000.

Exercise 9.2 (Identify the variable)

Identify the response variable (\(Y\)) and predictor variable (\(X\)) in each given relationship of interest.

  1. We want to use a person’s arm length to understand their height.
  2. We want to predict a person’s carbon footprint (in annual \(CO_2\)) emissions) with the distance between their home and work.
  3. We want to understand how a child’s vocabulary level might increase with age.
  4. We want to use information about a person’s sleep habits to predict their reaction time.

Answer

  1. \(X\) = arm length and \(Y\) = height.
  2. \(X\) = distance between home and work and \(Y\) = carbon footprint.
  3. \(X\) = age and \(Y\) = child’s vocabulary.
  4. \(X\) = sleep habits and \(Y\) = reaction time.

Exercise 9.3 (Interpreting coefficients)

In each situation below, suppose that the typical relationship between the given response variable \(Y\) and predictor \(X\) can be described by \(\beta_0 + \beta_1 X\). Interpret the meaning of \(\beta_0\) and \(\beta_1\) and indicate whether your prior understanding suggests that \(\beta_1\) is negative or positive.

  1. \(Y\) = height in cm of a baby kangaroo, \(X\) = its age in months.
  2. \(Y\) = a data scientist’s number of GitHub followers, \(X\) = their number of GitHub commits in the past week.
  3. \(Y\) = number of visitors to a local park on a given day, \(X\) = rainfall in inches on that day.
  4. \(Y\) = the daily hours of Netflix that a person watches, \(X\) = the typical number of hours that they sleep.

Answer

  1. For every one month increase in age, we expect the height to increase by \(\beta_1\) in cm. The \(\beta_0\) denotes the expected height when age equals to zero month.
  2. For every one commit increase in the past week, we expect the data scientist’s number of Github followers by \(\beta_1\). The \(\beta_0\) denotes the expected followers when commit equals to zero.
  3. For every one inch increase of rainfall, we expect the number of visitors to a local park to decrease by \(\beta_1\). The \(\beta_0\) denotes the expected number of visitors when rainfalls equals to zero.
  4. For every number one hour increase that they sleep, we expect the daily hours of Netfliz that person watches decrease by \(\beta_1\). The \(\beta_0\) denotes the expected hours of Netflix watches when number of hours of sleep equals to zero.

Exercise 9.4 (Deviation from the average)

Consider the Normal regression model (9.6). Explain in one or two sentences, in a way that one of your non-stats friends could understand, how \(\sigma\) is related to the strength of the relationship between a response variable \(Y\) and predictor \(X\).

Answer

Our data’s variability is measured by \(sigma\), which indicates that the lower the value, the less variable our data are. To give an example, if we know that our average data is 100 and that our variability is 10, we should anticipate that our data will vary by 10, demonstrating the tightness of our data and the strength of our predictor. The association between our predictor and outcome variables is weaker when our variability is 50, as opposed to low variability, which means that our data may vary by as much as 50.

Exercise 9.5 (Bayesian model building: Part I)

A researcher wants to use a person’s age (in years) to predict their annual orange juice consumption (in gallons). Here you’ll build up a relevant Bayesian regression model, step by step.

  1. Identify the Y and X variables in this study.
  2. Use mathematical notation to specify an appropriate structure for the model of data Y (ignoring X for now).
  3. Rewrite the structure of the data model to incorporate information about predictor X. In doing so, assume there’s a linear relationship between Y and X.
  4. Identify all unknown parameters in your model. For each, indicate the values the parameter can take.
  5. Identify and tune suitable prior models for your parameters. Explain your rationale.

Answer

Lorem

Exercise 9.6 (Bayesian model building: Part II)

Repeat the above exercise for the following scenario. A researcher wishes to predict tomorrow’s high temperature by today’s high temperature.

Answer

Lorem

Exercise 9.7 (Posterior simulation T/F)

Mark each statement about posterior regression simulation as True or False.

  • MCMC provides the exact posterior model of our regression parameters (\(\beta_0\), \(\beta_1\), \(\sigma\)).
  • MCMC allows us to avoid complicated mathematical derivations.

Answer

Lorem

Exercise 9.8 (Posterior simulation)

For each situation, specify the appropriate stan_glm() syntax for simulating the Normal regression model using 4 chains, each of length 10000. (You won’t actually run any code.)

  1. \(X\) = age; \(Y\) = height; dataset name: bunnies.
  2. \(Clicks_i|\beta_0,\beta_1,\sigma∼N(\mu_i,\sigma^2) \;\; with \;\; \mu_i = \beta_0 + \beta_1Snaps_i\); dataset name: songs.
  3. \(Happiness_i|\beta_0,\beta_1,\sigma∼N(\mu_i,\sigma^2)) \; \; with \; \; \mu_i = \beta_0 + \beta_1 Age_i\); dataset name: dogs.

Applied exercises

Exercise 9.9 (How humid is too humid: model building)

Throughout this chapter, we explored how bike ridership fluctuates with temperature. But what about humidity? In the next exercises, you will explore the Normal regression model of rides (\(Y\)) by humidity (\(X\)) using the bikes dataset. Based on past bikeshare analyses, suppose we have the following prior understanding of this relationship:

  • On an average humidity day, there are typically around 5000 riders, though this average could be somewhere between 1000 and 9000.
  • Ridership tends to decrease as humidity increases. Specifically, for every one percentage point increase in humidity level, ridership tends to decrease by 10 rides, though this average decrease could be anywhere between 0 and 20.
  • Ridership is only weakly related to humidity. At any given humidity, ridership will tend to vary with a large standard deviation of 2000 rides.
  1. Tune the Normal regression model (9.6) to match our prior understanding. Use careful notation to write out the complete Bayesian structure of this model.
  2. To explore our combined prior understanding of the model parameters, simulate the Normal regression prior model with 5 chains run for 8000 iterations each. HINT: You can use the same stan_glm() syntax that you would use to simulate the posterior, but include prior_PD = TRUE.
  3. Plot 100 prior plausible model lines (\(\beta_0 + \beta_1 X_i\)) and 4 datasets simulated under the priors.
  4. Describe our overall prior understanding of the relationship between ridership and humidity.

Answer

$$ \[\begin{gather*} Y_i | \beta_0,\beta_1,\sigma∼N(\mu_i,\sigma^2) \; \;with \;\;\mu_i=\beta_0 + \beta_1 X_i \\ \beta_{0c} \sim N(5000, 2000) \\ \beta_1 \sim N(-10, 5) \\ \sigma \sim Exp(1/2000) \end{gather*}\] $$

Code 
library(bayesrules)
library(tidyverse)
library(rstanarm)
library(tidybayes)
library(bayesplot)
library(broom.mixed)
library(patchwork)
library(janitor)

data(bikes)
bike_model_prior <- stan_glm(rides ~ humidity, data = bikes,
                       family = gaussian,
                       prior_intercept = normal(5000, 2000),
                       prior = normal(-10, 5), 
                       prior_aux = exponential(1/2000),
                       chains = 5, iter = 8000, prior_PD = TRUE)
bikes %>% 
  add_epred_draws(bike_model_prior, ndraws = 100) %>% 
  ggplot(aes(humidity, rides)) + 
  geom_line(aes(y = .epred, group = .draw), size = 0.1)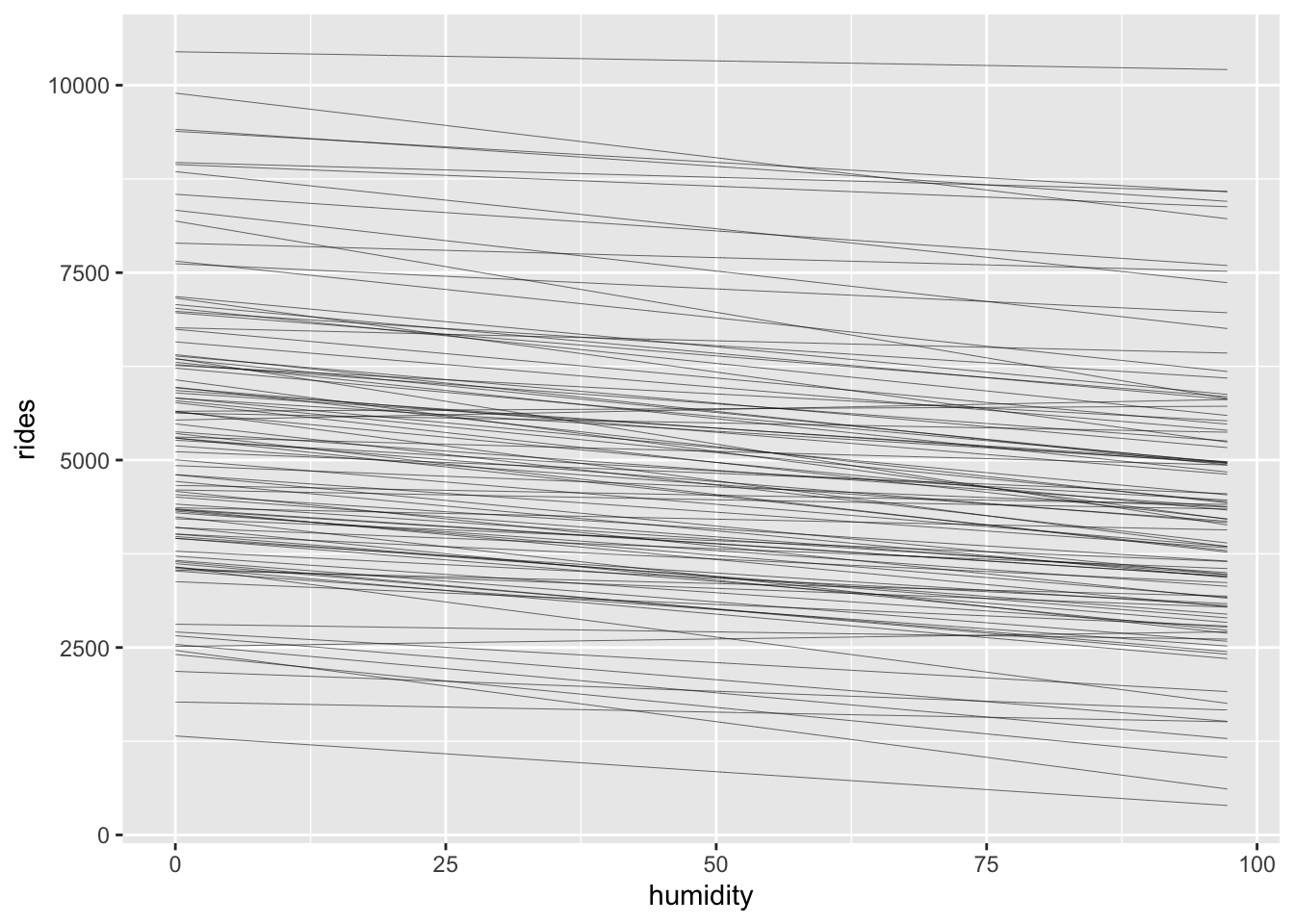

set.seed(12)

bikes %>%
  add_predicted_draws(bike_model_prior, ndraws = 4) %>% 
  ggplot(aes(humidity, rides)) + 
  geom_point(aes(y = .prediction, group = .draw), size = 0.2) + 
  facet_wrap(~ .draw)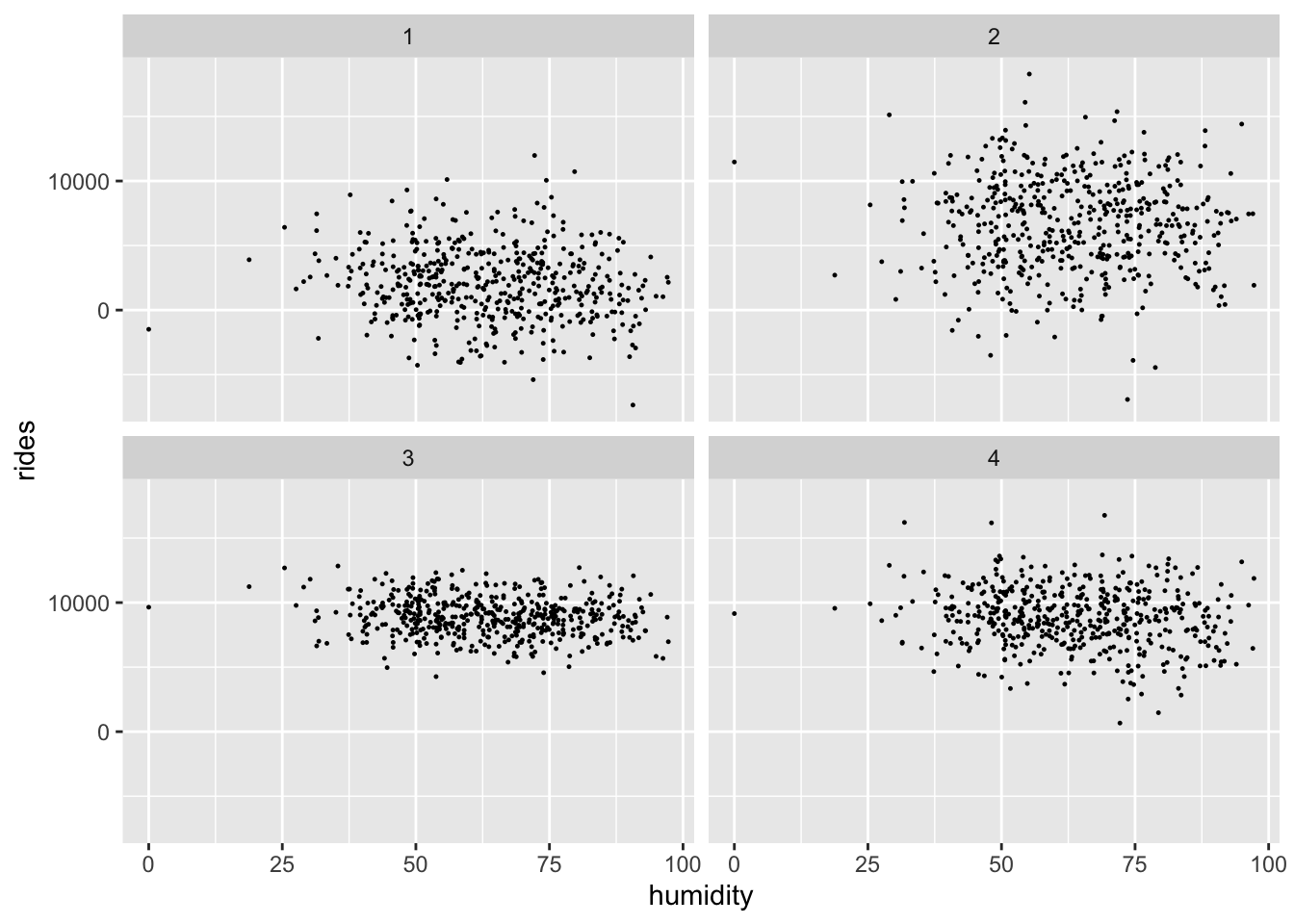

  1. our initial prior is that as the humidity increase, the number of rides on average are decreasing.

Exercise 9.10 (How humid is too humid: data)

With the priors in place, let’s examine the data.

  1. Plot and discuss the observed relationship between ridership and humidity in the bikes data.
  2. Does simple Normal regression seem to be a reasonable approach to modeling this relationship? Explain.

Answer

  1. The relationship between humidity and number of rides seems are not really clear, however fitting a linear model to the data showed that there are on average slight decrease in the number of ride in response to increase in humidity.
ggplot(bikes, aes(x = humidity, y = rides)) + 
  geom_point(size = 0.5) + 
  geom_smooth(method = "lm", se = FALSE)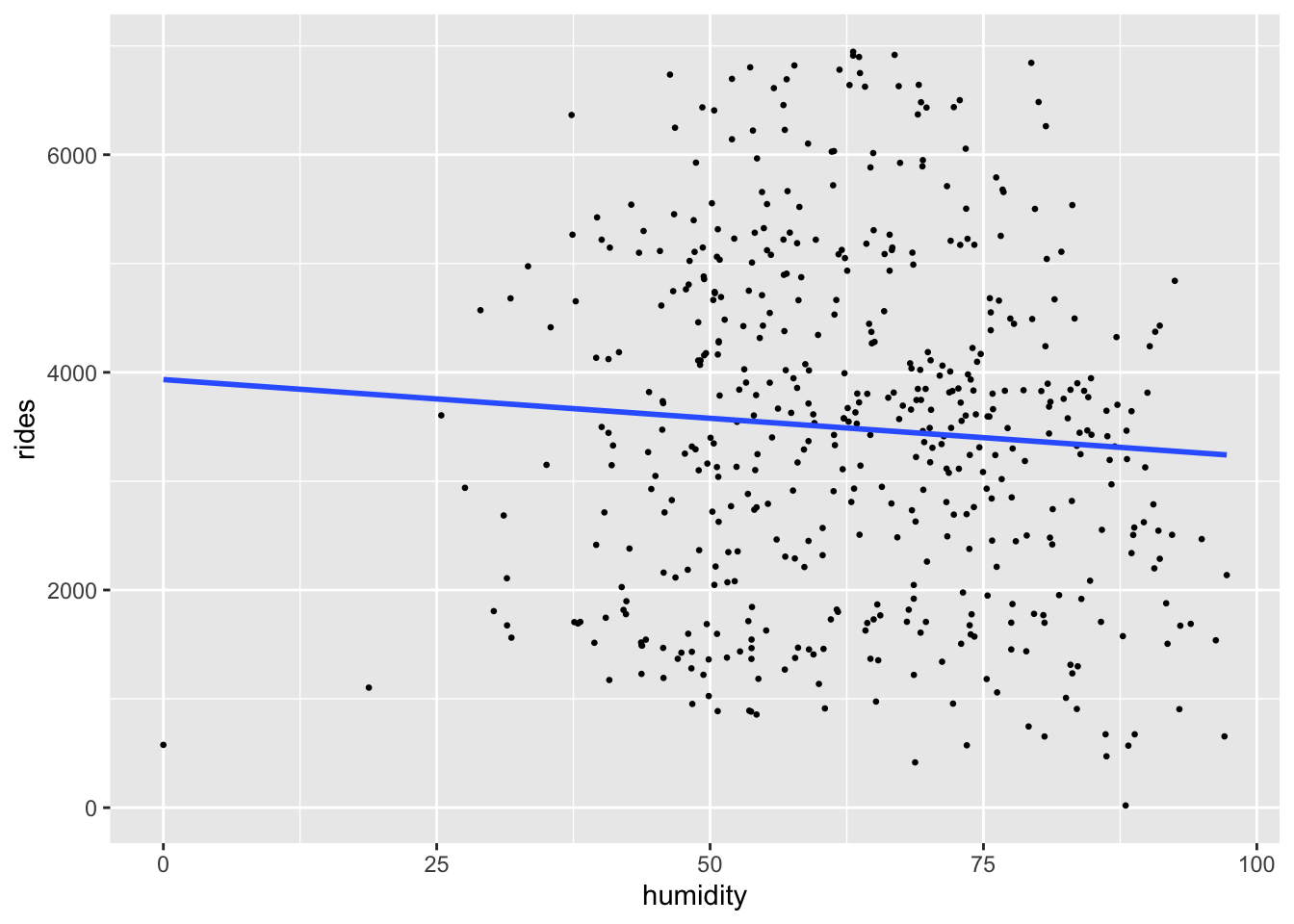

  1. Yes, since based on the figure above, we can see that there is slight negative linear relationship between the humidity and ridership.

Exercise 9.11 (How humid is too humid: posterior simulation)

We can now simulate our posterior model of the relationship between ridership and humidity, a balance between our prior understanding and the data.

  1. Use stan_glm() to simulate the Normal regression posterior model. Do so with 5 chains run for 8000 iterations each. HINT: You can either do this from scratch or update() your prior simulation from Exercise 9.9 using prior_PD = FALSE.
  2. Perform and discuss some MCMC diagnostics to determine whether or not we can “trust” these simulation results.
  3. Plot 100 posterior model lines for the relationship between ridership and humidity. Compare and contrast these to the prior model lines from Exercise 9.9.

Answer

bike_model <- update(bike_model_prior, prior_PD = FALSE)
  1. The result below shows that the effective sample size ratio and R-hat are very close to 1, indicating that the chains are stable and well-mixed. The trace plot and the density plot below show visually that the chains are well-mixed and stable.
# Effective sample size ratio and Rhat
neff_ratio(bike_model)
(Intercept)    humidity       sigma 
    1.01665     1.03015     1.04410 
rhat(bike_model)
(Intercept)    humidity       sigma 
  0.9999646   0.9999129   0.9998725 
# Trace plots of parallel chains
trace_plot <- mcmc_trace(bike_model, size = 0.1)

# Density plots of parallel chains
density_plot <- mcmc_dens_overlay(bike_model)

trace_plot / density_plot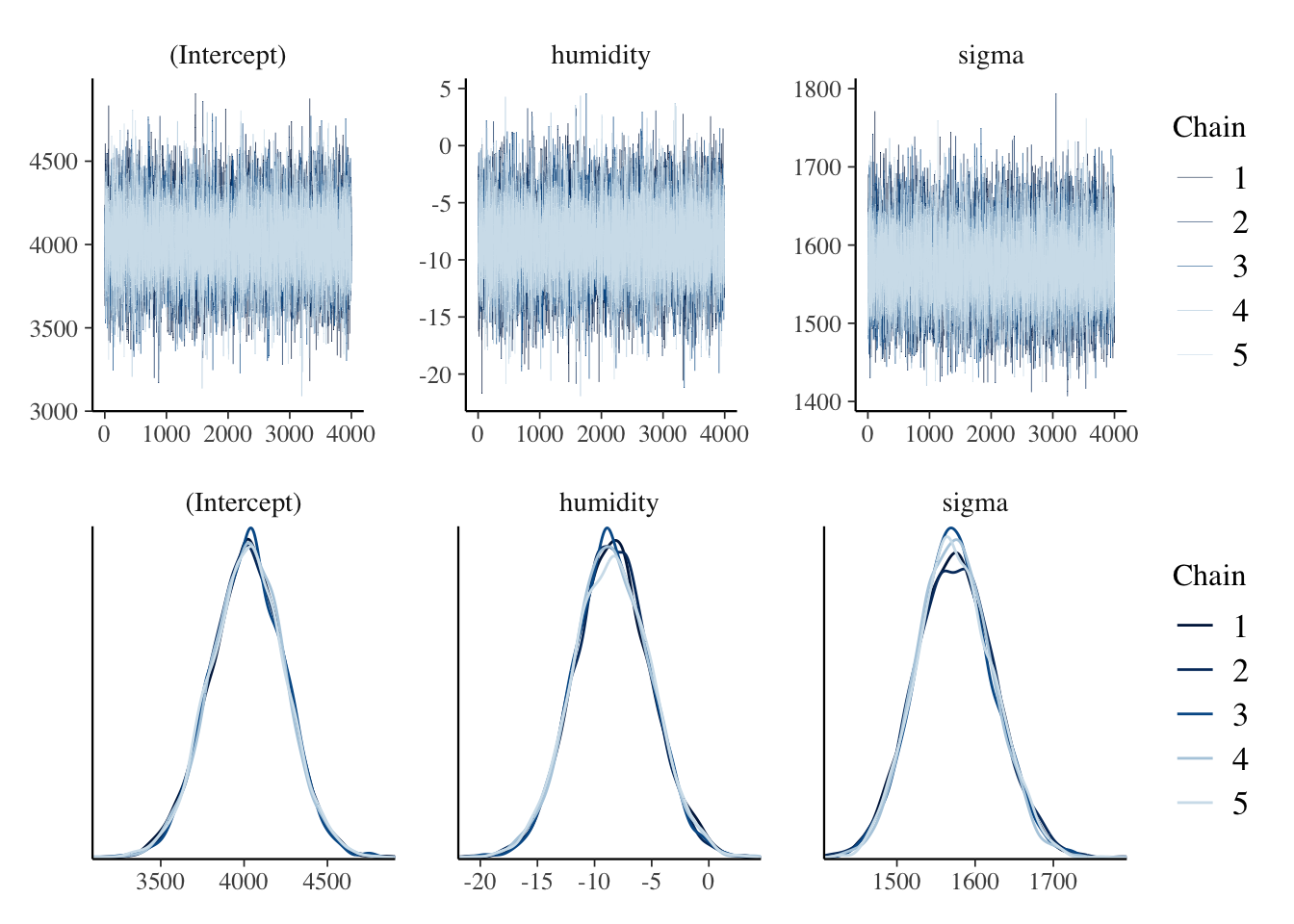

  1. Compare to the prior, the relationship between humidity and rides is steeper than we expected. Moreover, the posterior are less variable in comparison to the prior, in which we have more confident in the relationship between humidity and prior after conditioning on the data.
bikes %>%
  add_epred_draws(bike_model, ndraws = 100) %>% 
  ggplot(aes(x = humidity, y = rides)) +
    geom_line(aes(y = .epred, group = .draw), alpha = 0.15) + 
    geom_point(data = bikes, size = 0.05)

Exercise 9.12 (How humid is too humid: posterior interpretation)

Finally, let’s dig deeper into our posterior understanding of the relationship between ridership and humidity.

  1. Provide a tidy() summary of your posterior model, including 95% credible intervals.
  2. Interpret the posterior median value of the \(\sigma\) parameter.
  3. Interpret the 95% posterior credible interval for the humidity coefficient, \(\beta_1\).
  4. Do we have ample posterior evidence that there’s a negative association between ridership and humidity? Explain.

Answer

# Posterior summary statistics
tidy(bike_model, effects = c("fixed", "aux"),
     conf.int = TRUE, conf.level = 0.95)
# A tibble: 4 × 5
  term        estimate std.error conf.low conf.high
  <chr>          <dbl>     <dbl>    <dbl>     <dbl>
1 (Intercept)  4023.      225.     3580.    4457.  
2 humidity       -8.50      3.36    -15.0     -1.78
3 sigma        1573.       49.3    1480.    1672.  
4 mean_PPD     3483.       99.7    3291.    3678.

  1. Based on the table above, we estimated that the \(\sigma\) has a posterior median of 1573, with 95% credible interval of [1481, 1674]. That means we expect the ridership on a given day could be as high or as low as 1573 riders from the average ridership on the same day and the same humidity.

  2. The 95% credible interval indicates that the humidity coefficient (\(\beta_1\)) could be anywhere between -15 to -1.8.

  3. Yes, we have an ample evidence that there’s negative association between ridership and humidity. First, based on the visual inspection from the posterior we plotted above, we saw negative association between ridership and humidity. Had no association or positive association, the figure above would showed a flat or positive slope. Second, the posterior summary statistics for the humidity showed that the credible interval had no overlap with zero. Lastly, the quick tabulation from posterior probability showed that there’s almost certainly positive association between ridership and humidity.

bike_model_df <- as.data.frame(bike_model)

bike_model_df %>% 
  mutate(exceeds_0 = humidity > 0) %>% 
  tabyl(exceeds_0)
 exceeds_0     n percent
     FALSE 19877 0.99385
      TRUE   123 0.00615

Exercise 9.13 (How humid is too humid: prediction)

Tomorrow is supposed to be 90% humidity in Washington, D.C. What levels of ridership should we expect?

  1. Without using the posterior_predict() shortcut function, simulate two posterior models:
  • the posterior model for the typical number of riders on 90% humidity days; and
  • the posterior predictive model for the number of riders tomorrow.
  1. Construct, discuss, and compare density plot visualizations for the two separate posterior models in part a.
  2. Calculate and interpret an 80% posterior prediction interval for the number of riders tomorrow.
  3. Use posterior_predict() to confirm the results from your posterior predictive model of tomorrow’s ridership.

Answer

  1. As shown in the table below, the posterior model for typical number of riders on 90% humidity is 3260 with a 90% credible interval of [3035, 3483]. The posterior predictive model for number of riders tomorrow itself would be around 3247, with 90% credible interval of [185, 6320].
predict_90 <- bike_model_df %>% 
  mutate(mu = `(Intercept)` + humidity * 90,
         y_new = rnorm(20000, mean = mu, sd = sigma))

predict_90 %>% 
    summarize(
      median_mu = quantile(mu, 0.5),
      lower_mu = quantile(mu, 0.025),
      upper_mu = quantile(mu, 0.975),
      median_new = quantile(y_new, 0.5),
      lower_new = quantile(y_new, 0.025),
      upper_new = quantile(y_new, 0.975)
      )
  median_mu lower_mu upper_mu median_new lower_new upper_new
1  3259.577 3034.744  3483.41   3252.493  184.4085  6358.909
mu_plot <- predict_90 %>% 
  ggplot(aes(mu)) + 
  geom_density()

y_new_plot <- predict_90 %>% 
  ggplot(aes(y_new)) + 
  geom_density()

mu_plot + y_new_plot

Back to top

Reuse

Citation

For attribution, please cite this work as:
Reynaldo Hutabarat, Farhan. 2022. “Bayes Rules! Chapter 9 Exercises.” September 25, 2022. https://weaklyinformative.com/posts/2022-09-25-bayes-rules-chapter-9-exercises/bayes-rules-chapter-9-exercise.html.