On Lincoln Index

Introduction

Suppose you are writing a blog post, and you wanted to make sure there are no errors in the writing. You asked your colleague to review the blog post, and they found numerous errors. But, you can’t be sure if your colleague managed to spot all the errors. By asking your other colleague, you can estimate the number of errors even though they do not catch all the errors. How could that happen? This method is called the Lincoln Index. The Lincoln Index estimates the number of errors as:

\[ \text{expected errors} = \frac{E_1 E_2}{S} \]

where \(E_1\) and \(E_2\) are the number of errors found by reviewer 1 and reviewer 2, \(S\) is the number of common errors found by both reviewers. Let’s say from the story above, the first reviewer found 25 errors, the second reviewer found 15 errors, and they both found 5 errors in common. So, the number of errors is estimated around \(25 \times15 / 5 = 75\) errors. If you feel a little bit skeptical about the method, we could always resort to simulation to check if the method gives a reasonable estimate.

Simulation

Let’s assume that we know the \(N\) true number of errors in the blog post, which is 1000 errors. Instead of the number of errors found, each reviewer has \(p_1\) and \(p_2\) probability of finding errors. In this case, let’s set the \(p_1 = 30\%\) and \(p_2 = 20\%\).

TRUE_BUG_COUNT = 1000
p1 = 0.3
p2 = 0.2

For each iteration, we simulate whether the reviewer catch the error, denoted as p1_errors and p2_errors. And then, we count the common errors both reviewers found. Finally, we plug the numbers into the equation above. The code is written as:

from random import random, seed
import matplotlib.pyplot as plt

plt.style.use("ggplot")


def is_found(p):
    return 1 if random() < p else 0


def simulate(true_error_count, p1, p2, iterations=10_000):
    estimated_error_counts = []
    for _ in range(iterations):
        p1_errors = [is_found(p1) for _ in range(true_error_count)]
        p2_errors = [is_found(p2) for _ in range(true_error_count)]
        common_errors = [
            p1_error & p2_error
            for p1_error, p2_error in zip(p1_errors, p2_errors)
        ]
        estimated_error_count = (
            sum(p1_errors) * sum(p2_errors) / sum(common_errors)
        )
        estimated_error_counts.append(estimated_error_count)
    return estimated_error_counts

And as we pressed the simulate button, we found that the mean for the estimate bug is centered around 1000, our true number of errors. By simulating the data generating process, we also get the uncertainty on the number of errors.

from statistics import mean, stdev

seed(12)
counts = simulate(TRUE_BUG_COUNT, p1, p2)
print(f"Mean: {mean(counts):.2f}\n Std: {stdev(counts):.2f}")

Mean: 1008.58
 Std: 101.01

plt.hist(counts);
plt.show();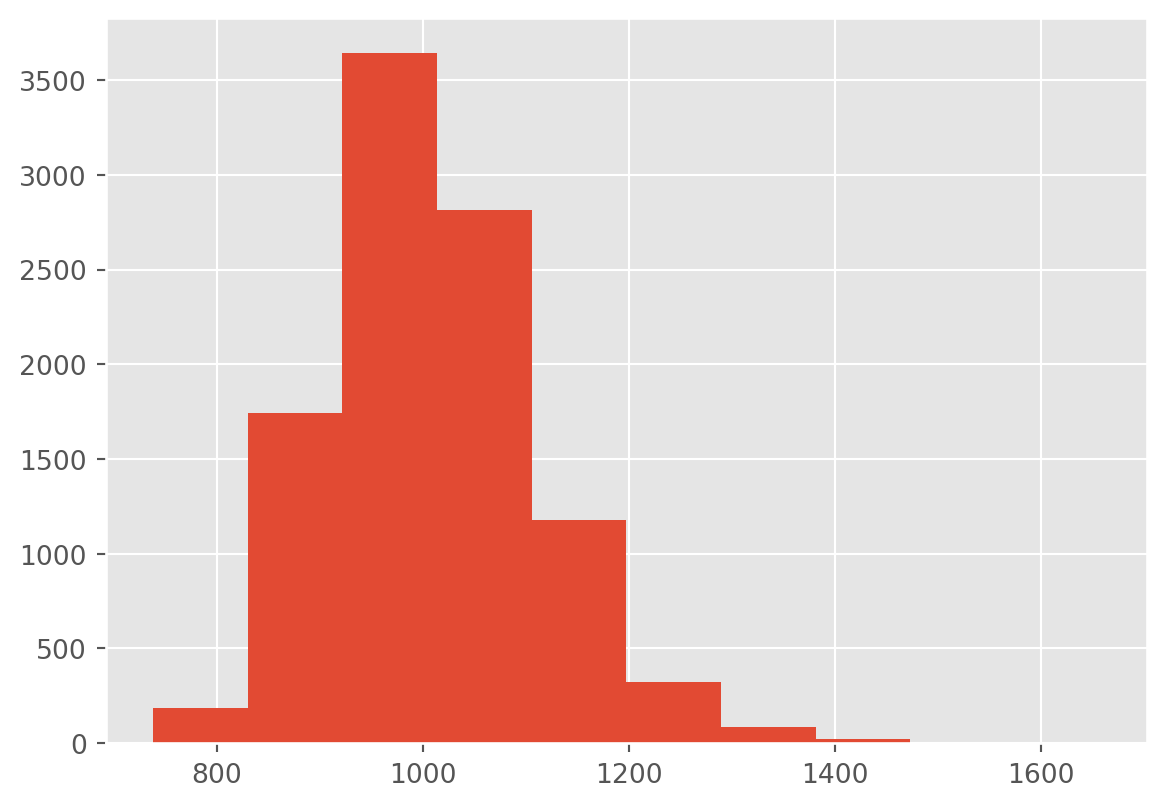

Conclusion

The Lincoln Index assumes that every error has an equal chance of being spotted. Moreover, if the probability of spotting the errors is low, then the denominator is more likely to be zero since the probability for the common errors is also low. In conclusion, the Lincoln Index is merely an estimate but a useful one.